Optimization

Episode #8 of the course Business analysis fundamentals by Polina Durneva

 

Hello! In the previous lessons, we primarily discussed different classification and prediction tools in business analytics. Today and tomorrow, we’ll shift our focus to two methods used in managerial science. These two methods significantly differ from all the previously discussed methods. Today, we will talk about optimization, and tomorrow, we will talk about simulation.

 

What Is Optimization?

Optimization is the process of finding the most feasible solution to a problem. To build an optimization model, you need to account for the following components:

• Decision variables are the unknowns that we try to solve for. For instance, we might have a problem in which we don’t know the numbers of stocks of different types to purchase for our portfolio to maximize return on investment. In this case, the numbers of different types of stocks are our decision variables.

• Objective function is the goal of our model. Using the example about stocks, we would have an objective to maximize our return on investment, so we would have a maximization function.

• Constraints are the limitations that apply to our decision. Again, speaking of stocks, we might have a limitation on the total number of stocks we can purchase (based on the amount of money we are ready to spend on stocks) or on the number of any individual stocks.

There are two types of optimization problems: linear and non-linear. From their names, it is not hard to guess that linear optimization deals with linear functions and non-linear optimization deals with non-linear functions (they also use different algorithms to max/min the objective function). Below are two examples for each type of optimization.

 

Linear Optimization

For instance, a company might have a budget of $100,000. This company is trying to decide how much of $100,000 to allocate to the marketing department and how much to the human resources department. From the money allocated to the marketing department, the company expects to earn 50%. From the money allocated to the human resources, the company expects to earn 70%. How much money should the company allocate to each department in order to maximize the company’s earnings if the marketing department requires at least $30,000?

This is a ridiculously simple optimization problem that wouldn’t require any advanced software (by the way, the Analytics Solver Platform [an add-in to Excel] is one of the most popular software in this area).

The decision variables would be the amounts of money that should be allocated to marketing and to HR. The objective would be to maximize earnings that are equal to 50%*(money for marketing) + 70%*(money for HR). In this problem, there will be only one constraint: The minimum amount of money for marketing should be at least $30,000.

The solution is quite simple. We will maximize our profit only if we spend $30,000 on marketing, and the rest on HR. If we didn’t have the constraint, we would maximize the profit be spending all money on HR.

 

Non-linear Optimization

Let’s assume that we have several distribution centers in our city, and we want to build one major warehouse somewhere in close proximity to the existing centers. The graph below illustrates the locations of our distribution centers.

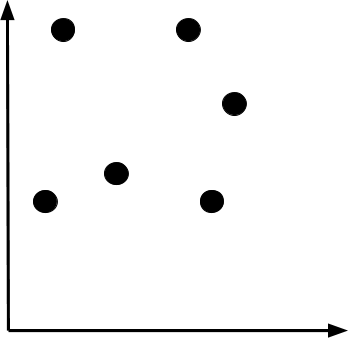
Where do you think would be the most optimal location of the warehouse? We can use optimization to identify it! The decision variables would be the coordinates of the new center. The objective would be to minimize the distance between the distribution centers and the new warehouse. Constraints would vary, but let’s drop them for the simplicity of our problem. Look at the graph below. What warehouse do you think has a more optimal location?

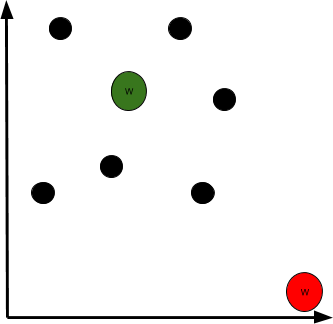
(The green one.)

 

Most Popular Applications of Optimization

Here are the most popular applications of optimization:

• Stock portfolio optimization. Optimization models can be used to create a portfolio of stocks by minimizing any risks associated with certain stocks.

• Transportation. We can use optimization to minimize costs associated with transportation of certain goods (by selecting the best combination of short routes).

• Call routing. Optimization can be used to route phone calls from one place to another.

That’s it for today. Tomorrow, we will discuss simulation.

Take care,

Polina

 

Recommended book

Good Strategy Bad Strategy: The Difference and Why It Matters by Richard Rumelt

 

Share with friends