Monte Carlo Simulation
Episode #9 of the course Business analysis fundamentals by Polina Durneva
Good morning! Today, we’ll discuss Monte Carlo Simulation, a modeling technique that accounts for uncertainty. Monte Carlo Simulation is named after Monte Carlo, a very famous casino resort in Monaco. The technique was introduced during the Second World War, when a group of scientists were working on the atom bomb. The scientists, John von Neumann and Stanislaw Ulam, used Monte Carlo simulation to explore the effects of neutrons that go through radiation shielding.
How Does Monte Carlo Simulation Work?
To understand how Monte Carlo Simulation works, let’s use an example.
Company A has produced 100 tables and expects to sell all of them during the next year. However, the price and the cost of each tables for the next year are uncertain. Company A is certain only about being able to sell all the tables. Moreover, looking at the historic price and historic cost, Company A’s analysts say that the price will range from $100 to $250, and the most likely value for price will be $120. As for the cost of tables, the analysts think that the cost will range from $50 to $100, and the most likely value for price will be $90. Our objective would be to estimate the possible profit of Company A after the company sells all of its tables.
Step 1: Determine uncertain parameters and their probability distribution.
(Probability distribution illustrates how likely each possible outcome is to occur.)
We know that for our problem, price and cost are uncertain parameters. For our case, we will use triangular distribution, whose graphs for each parameter are displayed below.
(The most popular probability distributions are normal, uniform, triangular, and discrete. For different cases, you will use different distribution.)
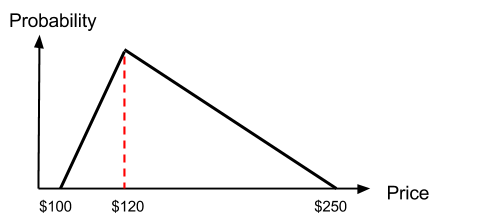

Step 2: Take random samples of uncertain parameters and calculate the output.
If we run Monte Carlo Simulation on any software (for instance, Analytics Solver Platform), we will have to choose how many times the software should randomly choose price and cost from the distributions above to calculate profit. The more repetitions we use, the more our probability distribution of profits will resemble normal distribution (a bell-shaped distribution with the center at its mean). Below is the graph of how our distribution of profits would look after many repetitions. The average of 1,000 repetitions would be the most probable value of profit for one unit.

Finally, we’ll receive the following results: The most probable price is $120 and the most probable cost is $90. After 1,000 repetitions, the average most probable profit will be close to $120 – $90 = $30 per unit.
This is, of course, is a very simple example. In real life, the applications of Monte Carlo Simulation are much more complicated and might have a bunch of uncertain parameters and other values in the model.
Most Common Applications of Monte Carlo Simulation
Here are the most common examples of the application of Monte Carlo Simulation:
• Risk-analysis. Monte Carlo Simulation is one of the most prominent risk analysis tools and is widely used in the areas with big ambiguity and uncertainty.
• Financial forecasting. We use Monte Carlo Simulation for financial forecasting, project management, and other areas.
That’s it for today. Tomorrow, we will finish our course by discussing other techniques in business analytics.
See you,
Polina
Recommended book
David and Goliath: Underdogs, Misfits, and the Art of Battling Giants by Malcolm Gladwell
Share with friends

