A Glimpse into Infinity: The Mandelbröt Set
Episode #10 of the course Great math problems for the 21st-century mind by John Robin
You may have seen this picture before:

Today, I’m going to explain the math that creates it and leave you with a breathtaking view.
This picture is none other than the Mandelbröt set. It might already look complex to you, but the complexity gets even better. If you zoom in to the space between the head and main body (the larger circular region shaped a bit like a heart), this is what you get:

And it goes on. If you zoom in on the spiral shapes that line the black circular region, you get this:
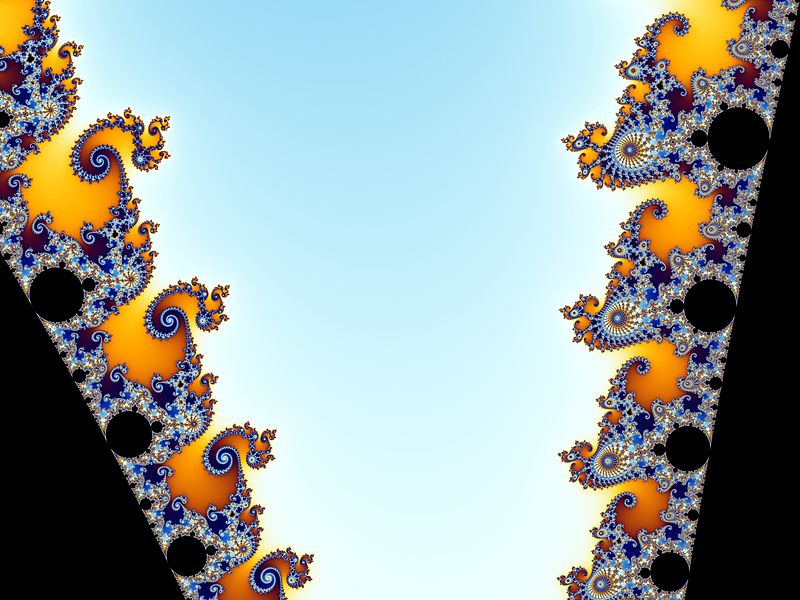
And closer, on one of the seahorse shapes themselves:

In fact, this pattern of awesome complexity goes on and on and on forever.
What’s most wondrous of all is this pattern is created by the simplest of mathematics, and now that we’ve taken a tour through the Riemann Hypothesis and understand what complex numbers are, we can close our course by appreciating how the giants of mathematics are not the only unsolved problems.
The Mandelbröt set is an example of what is known as a fractal, an infinitely repeating pattern. It is named after mathematician Benoit Mandelbröt. He did not invent the set, but thanks to the power of the computers at IBM, where he worked, he was able to create a visual representation in 1980 (much simpler than the picture here).
The set is created by mapping out a simple recursive function:
zn+1 = zn2 + c
where z and c are both complex numbers and z0 (i.e., the number we start with) is 0. A number, c, is said to be in the Mandelbröt set if the recursive function is bounded, meaning if we repeatedly calculate and find that it does not keep getting bigger and bigger, then we will keep it.
For example, let’s take the complex number c = 1 + i. Recall that this would be the same as writing the coordinate (1,1) on the xy-axis, where x is the real number and y is the imaginary.
Our recursive function would go like this:
z1 = 02 + (1 + i) = 1 + i
z2 = (1 + i)2 + (1 + i) = (1 + 2i − 1) + (1 + i) = 1 + 3i
(keep in mind that i2 = −1, since by definition, i = √−1)
z3 = (1 + 3i)2 + (1 + i) = (1 + 6i − 9) + (1 + i) = −7 + 7i
And so on. You can see that here, zn will keep growing larger. So, we will say that the point on the complex plane 1 + i is not in the Mandelbröt set.
Let’s try another, with the complex number c = 1/2 to see if it’s in the set. (Recall 1/2 = 1/2 + 0i.)
z1 = 02 + 1/2
z2 = (1/2)2 + 1/2 = 3/4
z3 = (3/4)2 + 1/2 = 17/16
z4 = (17/16)2 + 1/2 = 417/264
It’s not as easy to see, but if you try the next few out on your own, you’ll see that this one keeps growing, if a bit slower. So, 1/2 is not in the Mandelbröt set either.
Let’s try one more, with c = −1.
z1 = 02 − 1
z2 = (−1)2 − 1 = 0
z3 = (0)2 − 1 = −1
z4 = (−1)2 − 1 = 0
You can see that the pattern will repeat itself forever. We say that the recursive function is bounded by the number 1 because it will never grow any bigger in absolute size than 1. Therefore, the complex point c = −1 (i.e., -1 + 0i) is on the Mandelbröt set.
We can do this with every possible pair of complex numbers, a + bi (using a computer, of course). The reason why the patterns repeat no matter how much we zoom in is because you can think of any point a + bi as being surrounded by infinitely many points in a circular region around it. For example, 0.5 + 0.75i is surrounded by points like 4.49 + 0.749i and 5.51 + 0.753i, etc. For any point, we can zoom in to smaller decimal close points and putting them through the function, always find further bounds to the Mandelbröt set.
The real beauty, though, is the patterns themselves. It’s no wonder that of all the mathematical giants of the 20th century, the Mandelbröt set has been called by some, “the thumbprint of God.”
Thank you for following along! I hope you’ve had as much fun as I have and that this inspires you to investigate this most wonderful topic further.
Find out more about John and connect with him on his website.
Recommended video
If you want to see the Mandelbröt set zoomed in to being larger than the known universe and how the details continue to arise and patterns repeat, this video will show you more of the wonder of this set.
Recommended book
A New Kind of Science by Stephen Wolfram
Share with friends

